1. 前言

在抽样统计计算原理中，我们已经给大家介绍了统计抽样的指标是如何计算产生的，并且给出了正态分布的图示，让我们来回顾一下：

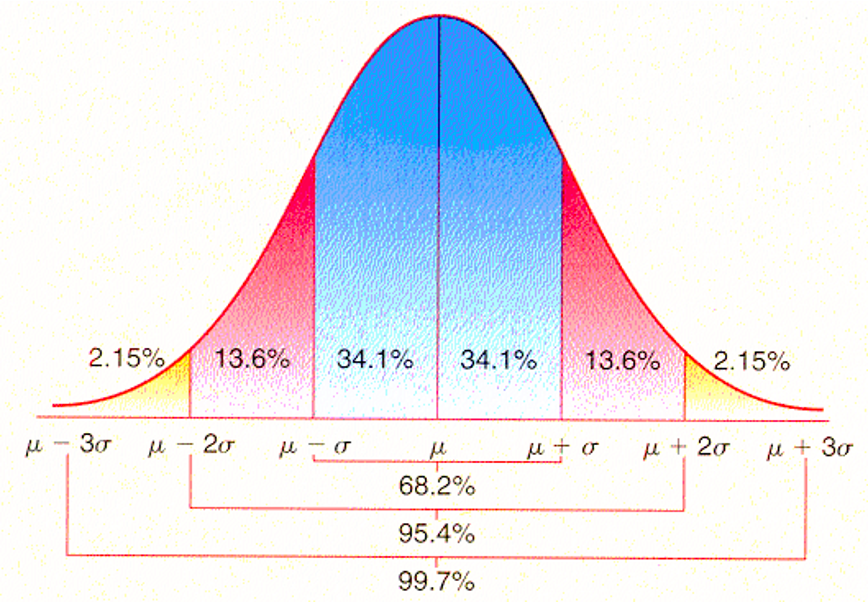
以上图示代表的含义是：

假设我们不知从何处得到一个样本（内含多个个体），在其抽样方法能够满足「符合正态分布」的条件下，对样本内的个体值计算其「均值」后，我们可以和「样本均值的均值」做比较，如果这个样本的「均值」离「样本均值的均值」比较远的概率是比较小的。基于正态分布曲线算得的数据：

落在距离「样本均值的均值」1倍「样本均值的标准差」以内的概率是「68.2%」
落在距离「样本均值的均值」2倍「样本均值的标准差」以内的概率是「95.4%」
落在距离「样本均值的均值」3倍「样本均值的标准差」以内的概率是「99.7%」

所以，如果这个样本的均值落在 3σ 之外，他的发生概率太小了（约为0.3%），以至于我们倾向于认为来自这个总体的样本均值不可能出现这种情况，所以这个样本一定是从别的总体里采集来的。但是它真的不是吗？宇宙之大无奇不有，也许就有那么一次出现了小概率事件，导致我们误会了这个样本。

因此，我们的判断存在四种可能性：

它的确属于原来的总体，但我们认为它不属于这个总体，我们错怪了它
它的确属于原来的总体，且我们也认为它属于这个总体，我们没有错怪它
它其实是来自别的总体，但我们认为它不属于别的总体，我们错怪了它
它其实是来自别的总体，且我们也认为它属于别的总体，我们没有错怪它

以上是我们可能出现的结果，其中1、3是我们判断错误的情况。我们当然不希望犯错误，如果一定有可能犯错误，至少我们也得评估下犯错误的概率有多大，确保我们犯错的姿势也能科学优雅，这就是我们去做假设检验的过程。

2. 假设检验

2.1. 假设检验是做什么的

要说假设检验，这其实是个古老的方法，近年由于 A/B Testing 大行其道，使假设检验方法迎来了新一波文艺复兴，因为一个严谨的 A/B Testing 的本质就是假设检验，那很多小伙伴都在问：假设检验是做什么的？那一堆似懂非懂的统计符号啥意思？首先假设检验解决的是对一个不确定的结论，从统计学的角度进行验证。无论是推翻旧结论还是验证新结论，都可以通过假设检验实现。

2.2. 什么时候适合做假设检验

关于推翻旧结论，当错误很明显的时候，不需要做假设检验。比如新上线一个首页设计后，一段时间内并没有别的业务发生变化，却观察得到首页的用户留资转化率直线下降。如果这个留资按钮的转化率持续下降，还有啥好说的，这时候不需要假设检验，直接开怼。

但总有些问题并不那么明显。如果同一时间，既有官网改版，又做了拉新运营活动，有多个变量同时发生，这个时候想要判断用户留资转化的下降到底是官网新设计不尽如人意还是运营活动起了反向效果呢，就无法直接得出结论了。此时就需要把用户按变量隔绝开做抽样检测，依次用假设检验方法看具体是哪个因素导致了用户留资转化下降的。

在论证新点子很好的时候，也需要先把新点子做出来，再做小范围测试。此时也要用假设检验方法。总之，假设检验方法适合于抽样检验/小范围测试的场景。

2.3. 假设检验是怎么做的

众所周知：证伪比证真容易多了。证真要穷尽各种可能，证伪只要找到反例即可。假设检验的基本思路也是如此，它利用了「小概率事件，不可能在一次小范围抽样中发生」的朴素原理（没错，就是上一章节我们提到的那种观点），先提一个假设，之后看能否用小概率事件推翻它。能推翻的，就说明假设不成立；不能推翻，就至少说明目前仍然缺乏证据。

基于这个原理，我们一般把要怼翻的结论，作为原假设，然后试着去怼翻它！

场景描述：我们想证明经过我们对首页的重新设计，新首页的留资转化率比老首页有所提升。接下来我们用假设检验来证明这个结论。

步骤①：明确试验假设

原假设：新首页转化率 - 老首页转化率 = 0% （我们希望推翻的结论）
备择假设：新首页转化率 - 老首页转化率 <> 0% （我们希望证明的结论）

步骤②：找小概率事件推翻「原假设」

做小范围抽样统计，如果抽样得到转化率提升值足够大，大到我们认为，如果新旧首页没有差异的话，这那么大的数值提升是不可能发生的，因此如果出现了，那极大可能是因为新首页设计的更好。

2.4. 什么时候可以推翻？什么时候应该接受？

看到步骤②大家可能会有疑问，如何推翻原假设呢。这个就比较复杂了，不同的情况有不同的统计学公式进行计算。同学们只需要知道做 A/B 测试的绝大多数情况下是通过一个「Z 检验」或「 T 检验」来完成的。Z 检验会得出一个计算结果叫 Z 值，T 检验会得出一个计算结果叫 T 值，我们只需要对比这个结果值落在哪个区域，就知道是否能够推翻原假设了。

如下图 Z 检验结果，我们只需要看值落标准正态分布密度函数图的左边中间还是右边，来判断。图中左中右三块是如何划分的呢，详情可见下一章置信区间。

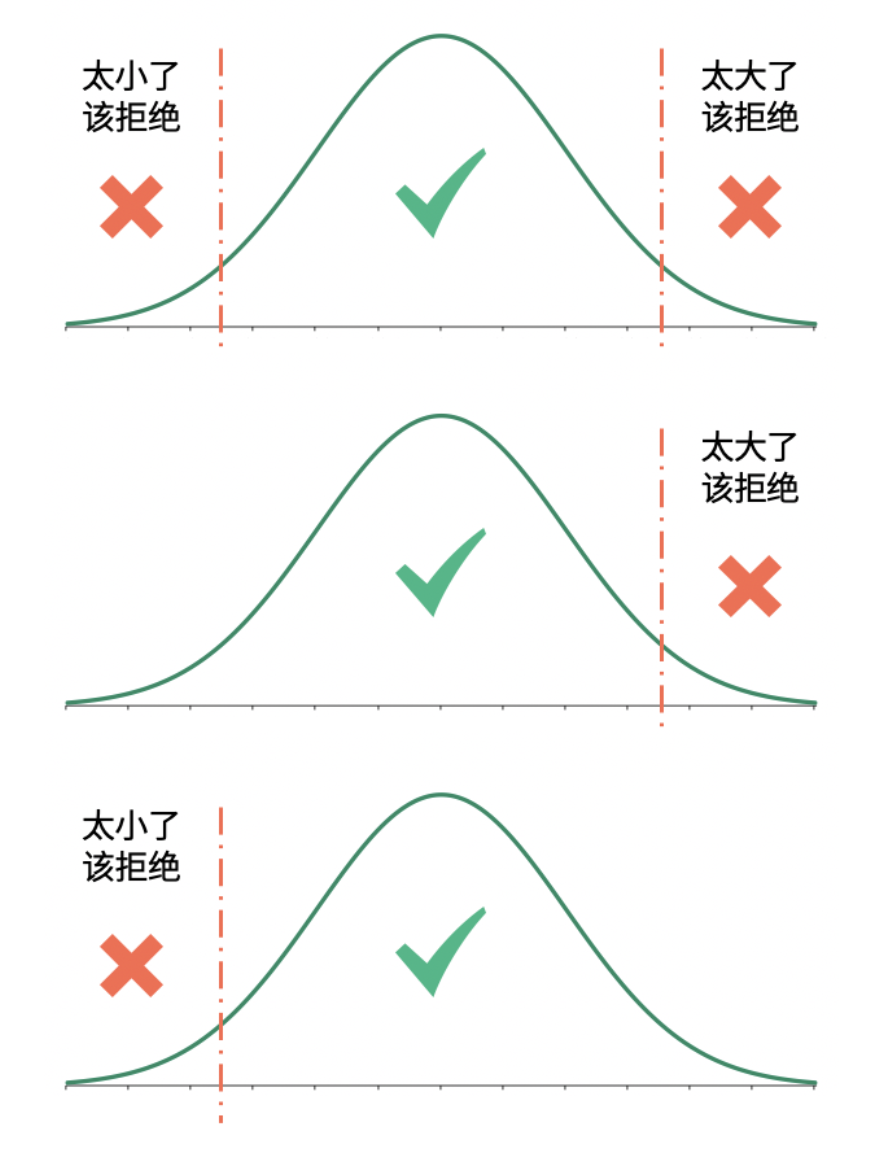
至于为什么有三种拒绝区域呢，主要是根据原假设的符号来判断，原假设中是 “=” 表示一个双尾试验适用第一个拒绝区域。原假设中是 ">=" 表示单尾试验适用第二个拒绝区域。原假设中是 “<=” 同理适用第三个拒绝区域。

关于拒绝区域，有个简单的记忆方法，就是：

如果原假设是等号，拒绝区域就是左右两侧。潜台词就是：既然咱俩相等，那检验值应该不大不小才对。
如果原假设是小于号，拒绝区域就是右侧。潜台词就是：既然你比我小，那检验值肯定不太大呀
如果原假设是大于号，拒绝区域就是左侧。潜台词就是：既然你比我大，那检验值肯定不能太小呀

当然，有很多统计软件/算法直接给了 P 值，P值是另一种判断是否推翻原假设的方式。

绝大部分情况下，大家记得：P 值小于 0.05 就拒绝原假设即可。

3. 置信区间

由于“置信区间”是“区间估计”中的一个概念，而讲“区间估计”之前，得先介绍“点估计”。

3.1. 点估计

“估计”是指用样本的数据估计全体的数据情况。之所以这么做，是因为很多时候，想全体采集数据太难了，又或者采集全体数据不现实，万一这个方案不好又推给全量用户会导致营收下降！所以必须抽样。
那么，直接用单回抽样数据值代表全体数据，就是所谓的”点估计“。
常见的点估计指标有2种：

人均值：比如经抽样得到的一个人群，这些人对某个图标按钮的人均点击次数是3次（按钮总点击次数 / 人群人数）。
转化率：比如经抽样得到的一个人群，这些人对某个转化页面中进入下一步的按钮的点击转化率为10%（按钮点击人数 / 页面浏览人数）。

但是，只使用一个抽样人群得到的数据值直接对总体进行估计是有问题的。哪怕每回抽样再随机，抽样对象不同，点估计值总会有细微差异，比如某按钮点击转化率指标，如果重复做5回随机抽样（抽5组人群分别计算），可能会得出5个不同的转化率，到底哪个转化率才能代表全体用户呢？为了解决这个问题，有了区间估计的做法。

3.2. 区间估计

通俗地讲：区间估计是在点估计的基础上，给一个合理取值范围。
例如：

我们预计某个页面按钮的点击转化率为10%（这是进行点估计）
我们预计某个页面按钮的点击转化率在8.5%～11.5%之间（这是在进行区间估计）

使用一个数值范围来进行估计，我们对于总体的实际数值会不会落在这个范围内就变得更有把握了。

3.3. 置信区间

在上述例子中，“ 8.5%～11.5% ”就称为置信区间，这很符合人们的常规理解：点估计的值很难 100% 准确，而使用一个数值范围则能使结论变得更加严谨。但这个范围又有多大可信度呢？人们用「置信水平」来衡量，即为：

“我们有多大把握，实际数值会落在置信区间内。”

「置信水平」一般用（1-α）表示。如果 α 取0.05，则置信水平为 0.95，即 95% 的把握。将置信区间与置信水平连起来，完整的表达即为：

“我们有 95% 的把握，该按钮曝光点击转化率的实际值会落在 8.5% 至 11.5% 之间。”

有小伙伴会好奇，为啥置信水平不是 100% ！通俗地说，当置信水平太高时，置信区间会变得非常大，从而产生一些正确但无用的结论。比如，置信水平是 100%，我们百分百确认该按钮的点击转化率在 0 到 100% 之间，虽然正确，但是句废话，并没有什么实际作用。

3.4. P值

从上文中我们知道，我们正在寻找小概率事件来推翻原假设，那么当前事件发生的可能性如果足够小，小到超过了某个数值，比如5%，我们就可以判定是小概率事件发生了，应推翻原假设！所以P值就是在衡量「当前事件发生的可能性，但含义是类似的」。

举个例子，我现在中了500万大奖，从数学上看有100万人参加，我的中奖概率是「百万分之一」。因此，当前事件P值是「百万分之一」，小概率事件已经发生了！（虽然这个例子不符合正态分布，但含义类似）

因此，P值越小，代表当前事件发生的可能性越小，但既然它能够发生，我们越有把握认为这是小概率事件，可以去怼原假设了。具体应该小到多少，常用的界限有1%、5%、20%，如果你要求P值越小，你能够正确推翻原假设的证据就越充足。

3.5. 统计功效

在统计理论中，统计功效Power = 1–β，因为 β表示发生第二类错误的概率，也就是说如果试验组和对照组的指标事实上是不同的，那么Power就表征能够探测到两者不同的概率（证明显著性是真实存在的概率）。

下面我们通俗来讲统计功效的显示意义，如果通过计算发现统计功效较低，那么此时可能会出现两种情况：

在试验结果显著时，我们能够正确判断的概率降低，判断错误的概率上升，也就是说此时试验结果可能并不一定是真实显著的。
在试验结果不显著时，但实际真实情况可能是差异显著的，从而错过了真实效应。

在 A/B 测试中，通常认为功效达到80%时，试验结果是真实可信的。

4. 常见问题列表

4.1. 为什么神策使用的是置信区间而不是P值？

答：因为「P值」只能够衡量「当前事件」发生的可能性，但「置信区间」能够带给我们更多「业务信息」。

假如我们得到一个P值0.01，它代表的含义是，我们确实有很高的把握推翻原假设，即认为两个分组（试验组、对照组）确实存在差异。但是试验组是更高还是更低？他的取值范围是多少？这些都无法通过P值得到。

而置信区间可以告诉我们，相比于对照组，我们的试验组确实有差异，而且知晓该试验组的指标是更高还是更低，同时，它相比于对照组的变化范围是「 x.x%～x.x%」，而这个区间也方便换算为业务指标的变化区间，方便我们得到更直接的「业务信息」。

4.2. 神策使用的是单尾检验还是双尾检验？

答：我们采用的是双尾检验。因为指标高低并不直接代表好坏，并不是说越高就越好，也许我们改善的是退货率或者崩溃率，这种场景下是越低越好，所以我们使用双尾检验，能够更好的体现指标变化的方向。甚至有些时候，我们会额外关注那些变差的版本，总结经验教训，如果使用单尾检验，我们就无法知道哪些版本是明确变差的。